해당 강의노트는 김성범 교수님의 Exponential Smoothing (지수 평활법) 강의를 기반으로 작성했음을 밝힙니다.
구간 평균법
- $L_t = {D_t + D_(t-1) + ... + D_(t-N+1)}/N$
- 과거 시점의 일정기간의 평균(단순 평균)으로 다음 시점을 예측
구간 평균법이 적절한 case
- Trend나 Seasonality variables과 같은 일정 패턴없이 변하는 level을 가진 데이터
(질문) 일정 패턴없이 변하는 level이 cycle인지 아니면 random한건지? 어떤 case를 의미하는 것인지 궁금
구간 평균법의 한계
- 과거 n개의 데이터에 동일한 가중치를 준다.
- 예시: 현재 시점 t를 기준으로 n=3까지의 과거 데이터를 고려한다고 가정해보자. 구간평균법은 t, t-1, t-2이 오래된 시점의 데이터인지 최신의 데이터인지 고려해주지 않고 일괄적으로 평균을 계산한다.
- 미래의 예측값이 모두 동일하다. (?)
구간 평균법에서 구간(N) 결정
- N이 작은 값일 때, 최근 데이터의 경향을 반영
- N이 큰 값일 때, 과거 데이터의 경향을 반영하여 편평하게 예측
- 경험적으로 판단하는 값
지수 평활법(Exponential Smoothing)
- 가중 평균 이용
- 지수분포 모양에 근거한 가중치 결정
- 최근 데이터의 경향에 보다 많은 가중치를 주고, 과거 데이터일수록 가중치가 줄어든다.
단순지수 평활법
- $L_0 = {D_t + D_(t-1) + ... + D_(t-N+1)}/N$
- $L_(t+1)$ 계산할 때 $(t=0, ... ,n)$
$L_(t+1) = \alpha*D_(t+1) + (1-\alpha)L_t$ - 모든 과거 데이터 포함하여 계산 => 구간 평균법과의 차이점: N개의 과거 데이터만 고려
- 최근 데이터에 보다 큰 가중치를 부여한다.
단순지수 평활법의 한계
- 구간 평균법과 동일한 한계점을 가진다.
- Trend나 계절적 변동 있는 데이터에 적합하지 않음.
- 미래의 예측값이 모두 동일하다.
- 구간 평균법 보다는 조금 더 정확할 수 있다. => 이유: 과거의 데이터에 동일한 가중치를 주기 보다, 지수적으로 가중치를 주는 방식으로 평균을 계산하기 때문
단순지수 평활법에서 $\alpha$ 결정
- smooth data라면, 큰 $\alpha$값 사용 => 최근 데이터에 보다 큰 가중치 적용
- nosiy data라면 $\alpha$값 사용 => 과거 데이터에 보다 큰 가중치 적용
- 보편적으로 $\alpha=0.2$나, $\alpha=0.3$ 사용
- R, python에는 최적의 $\alpha$값을 자동적으로 계산해주는 라이브러리 있음
이중지수 평활법
- Trend가 존재하는 시계열 데이터 예측시 적합
- 단순지수 평활법을 2번 적용
- 단순 회귀분석을 통해 $L_0$(기울기)와 $B_0$(Y절편) 결정
- 종속변수(Y): 관측값
- 독립변수(X): 시간 인덱스 $(1,2, ..., t)$
- Determine $L_(t+1)$ Smooth with $\alpha$
$$L_(t+1) = \alpha*D_(t-1)+(1-\alpha)(L_t + B_t)$$- $\alpha*D_(t-1)$ : Newly observed time series value
- $B_t$: Growth rate = "Trend"
- Determine $B_(t+1)$ Smooth with $\beta$
$$B_(t+1)=\beta(L_(t+1)-L_t)+(1-\beta)B_t$$- L_(t+1)-L_t : Difference between the levels in period t+1 and t
- $B_t$ : Growth rate made in time period t
- Forecast (renumber forecast time periods)
- $F_(t+n)=L_t+nB_t$
- n: 미래 t
- $F_(t+n)=L_t+nB_t$


(질문) $Y=\beta_0 + \beta_1*x^t$ Y절편을 유도하는 식이 등비급수를 통해 유도되는데, 해당 블로그 설명에서 확인했을 때 시정수(타우)를 의미하는 것인지 궁금하다.
홀트-윈터(Holt-Winter)지수 평활법
- 3중지수 평활법
- 계절 변동 존재시 사용
- Additive method(+-): 주로 덧셈/뺄셈은 선형적인 모델의 경우, seasonal variations가 일정(constant)할 경우
- Multiplicative method(*/): 주로 비선형적인, 좀 더 복잡한 패턴의 경우, seasonal variations가 증가할 경우

Additive 홀트-윈터(Holt-Winter)지수 평활법
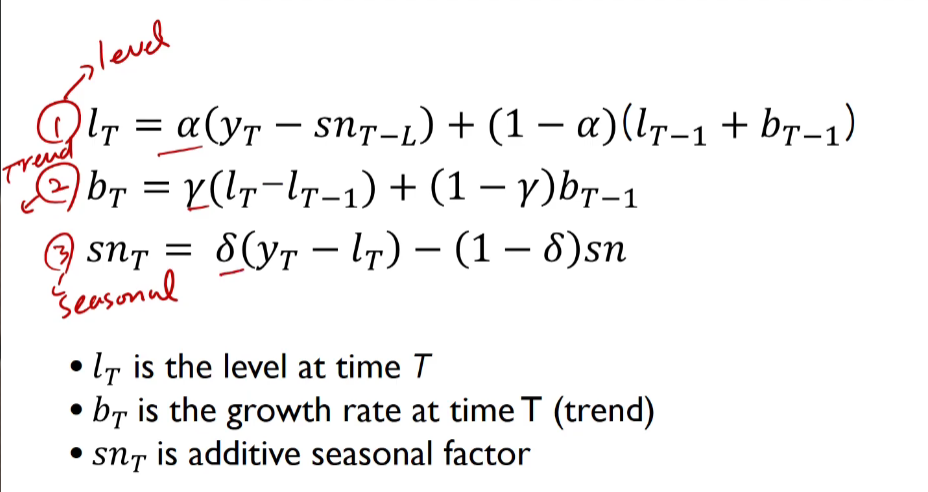
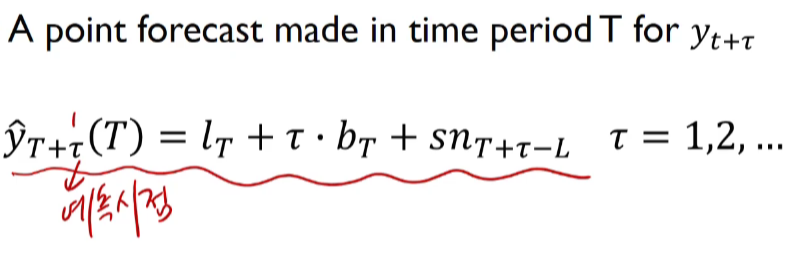
Multiplicative 홀트-윈터(Holt-Winter)지수 평활법
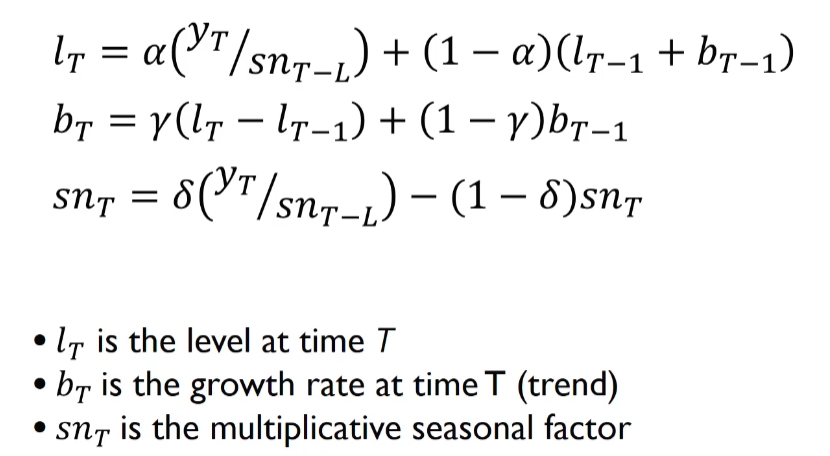
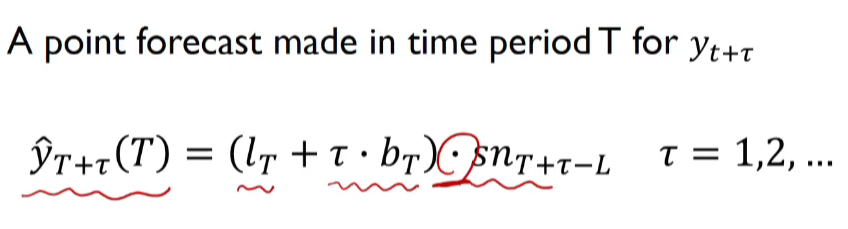
시계열분석 정리집: https://support.minitab.com/ko-kr/minitab/18/help-and-how-to/modeling-statistics/time-series/how-to/double-exponential-smoothing/methods-and-formulas/methods-and-formulas/
통계 - 지수평활방법: https://developer-ellen.tistory.com/14
통계 - 이중지수평활법: https://datalabbit.tistory.com/76?category=1146956
![[시계열] Exponential Smoothing (지수 평활법)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FEFcM7%2Fbtq5lzwb3rL%2Fyg6Ng0vMuUvuxhKYZPrF6K%2Fimg.png)