[시계열] Time Series Regression - Part 3

본 강의노트는 김성범 교수님의 Time Series Regression - Part 3를 바탕으로 작성했음을 밝힙니다.

Modeling Seasonal Variations Using Binary variables

• Binary variables: 0 아니면 1의 값을 가지는 변수

Example - Modeling Seasonal Variations Using Binary variables

호텔 투숙객 자료 

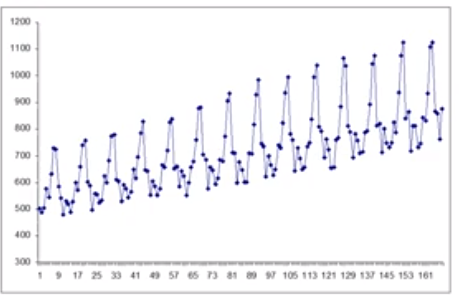
• 14년: 1년이 12개월이므로 t는 1~168
• Increasing Seasonal
  ⇒ log 변환 필요, 복원해줄땐 exlog 변환 필요

이를, 모델링할 수 있는 형태로 바꾼다면? 최소제곱법을 사용한 다중회귀모델

다중회귀모델 모델링식

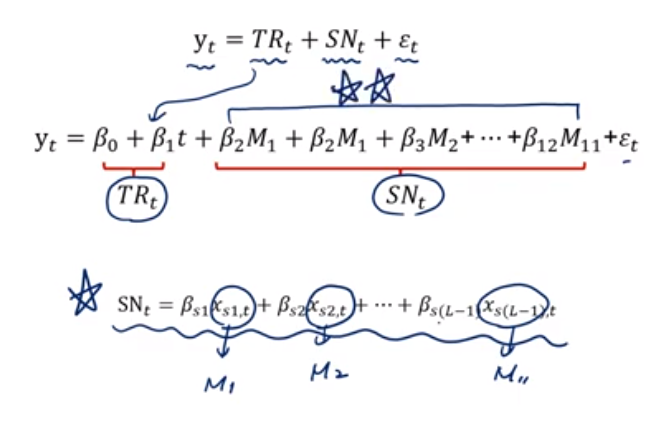
여기서, Binary variable은 M에 해당한다.

Example Modeling 결과

• Trend성분은 Linear한 B1, B2까지만 해당한다.
• B2는 기준이 12월(000..00)이므로 12월에 비해서 증감량을 비교할 수 있다.
• B2가 Positive하면, 1월이 12월보다 더 투숙객 수가 많은 것을 의미한다.

Trigonometirc Models

• sin과 cos 함수 활용한 모델

Trigonometirc Models

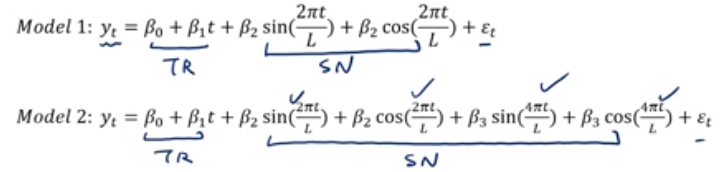
• Model1은 상대적으로 regular seasonal time series에서 사용한다.
• Model2는 상대적으로 복잡한 seasonal patterns에서 사용한다.

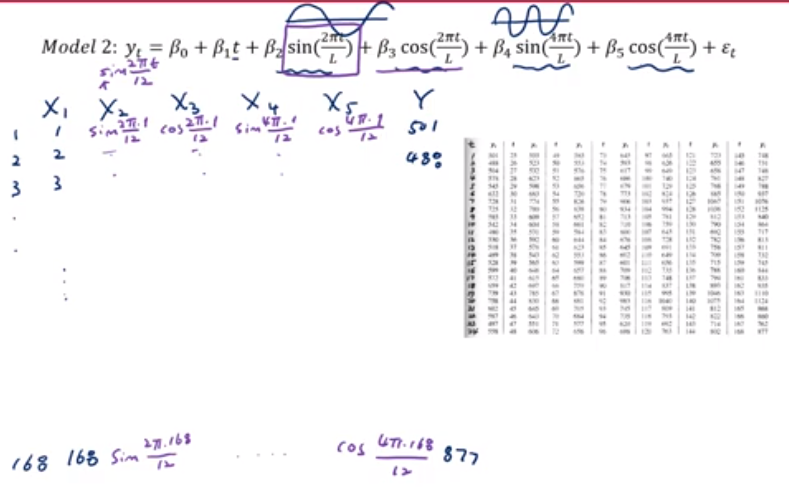
Example - Trigonometirc Models

Model1과 Model2

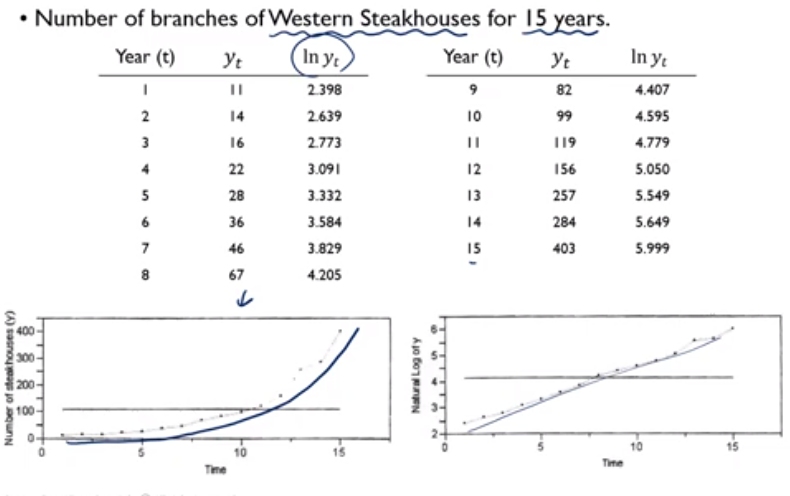
Growth Curve Models

• none linear해서 모델링하기 어렵다.
• 양변에 log를 취해주면 곱셈을 덧셈으로 표현 가능(선형 관계)해지고, 회귀 모델링할 수 있어진다.

Growth Curve Models

B값에 따른 Growth Curve

Growth curve 

• 0<B1<1: 비선형적으로 감소하는 커브
• B1>1: 비선형적으로 증가하는 커브
• B0: 어디서 시작할지

Example - Growth Curve Models

Example - Growth Curve Models

Example - Growth Curve Models Modeling 결과

Time Series Regression with Autocorrelation

• Error Term: 서로 다른 시점에서는 Cohierence = 0 즉, 독립이여야한다.
• 그러나 실제 모델에서는 시간에 의존적인 경우가 많다. ⇒ Autocorrelation을 고려해줘야한다.
• Autocorrelation 여부 확인방법: residual plots, Durbin-Watson test

First-order Autoregressive Process

• 가정: 회귀모델의 Error term이 Autocorrelate하다.
• a_t: 모델의 error term
• pi_1: 한 시점 차이의 autocorrelation의 크기, pi_1이 양수면, positive autocorrelate

First-order Autoregressive Process

Modeling 결과

• But, 최소제곱법을 적용할 수 없다.

Example - First-order Autoregressive Process

40:20