[시계열] Time Series Regression - Part 2

본 강의노트는 김성범 교수님의 Time Series Regression - Part2를 바탕으로 작성했음을 밝힙니다.

Review - 시계열 데이터 구성요소 

3가지 시계열 데이터 구성요소

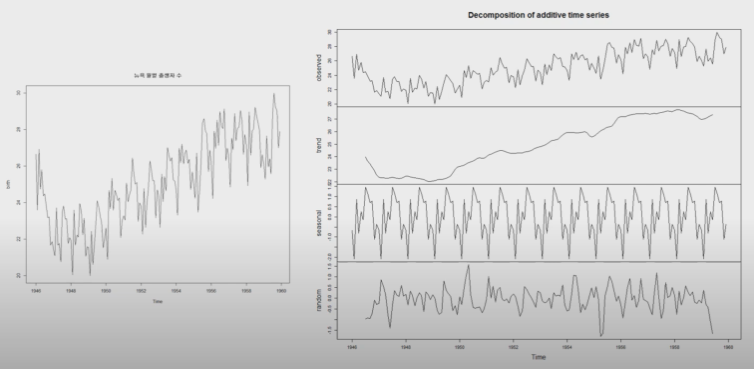
위의 그림을 보면, Trend, Seasonal variations, Random fluctuation이 나타남을 볼 수 있다. 

Time Series Analysis 

• 시계열 회귀분석 
• 지수 평활법 
• 박스-젠킨스 시계열 분석법
• 다양한 머신러닝 방법(Hidden Markov, DNN ...)

Time Series Regression Models(시계열 회귀분석)

t 시점에서의 종속변수(주로 y)에 대한 독립변수(주로 x)의 선형결합 

$y_t = TR_t + ε_t$

• $y_t$ = the value of time series
• $TR_t$ = the trend
  1. No trend, $TR_t = β_0$ <=> t의 함수가 아니다, t에 따라 변하지 않는다, t와 어떠한 관계가 성립되지 않는다. 
  2. Linear trend, $TR_t = β_0 + tβ_1$
  3. Quadratic trend, $TR_t = β_0 + tβ_1 + (t^2)*β_1$
• $ε_t$ = error term 

No Trend Model

Trend가 없는 모델은 오히려, y값들의 평균값을 계산하여 일괄적인 예측을 하는 것이 정확도가 높을 수 있다. 이러한 하나의 값으로 예측하는 것은 point forcasting이라고 한다. 

• prediction interval: 신뢰구간

예시. 대구 어획량

Kth Order Polynomial Time Series Regression Models

Trend가 있는 일반적인 시간에만 의존적인 시계열 모델

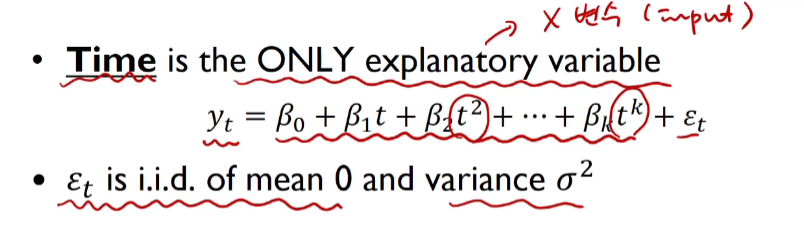
최소제곱법 

Loss(제곱 오차의 합)가 가장 작은 예측값을 찾는다. 

최소제곱법

Trend Model

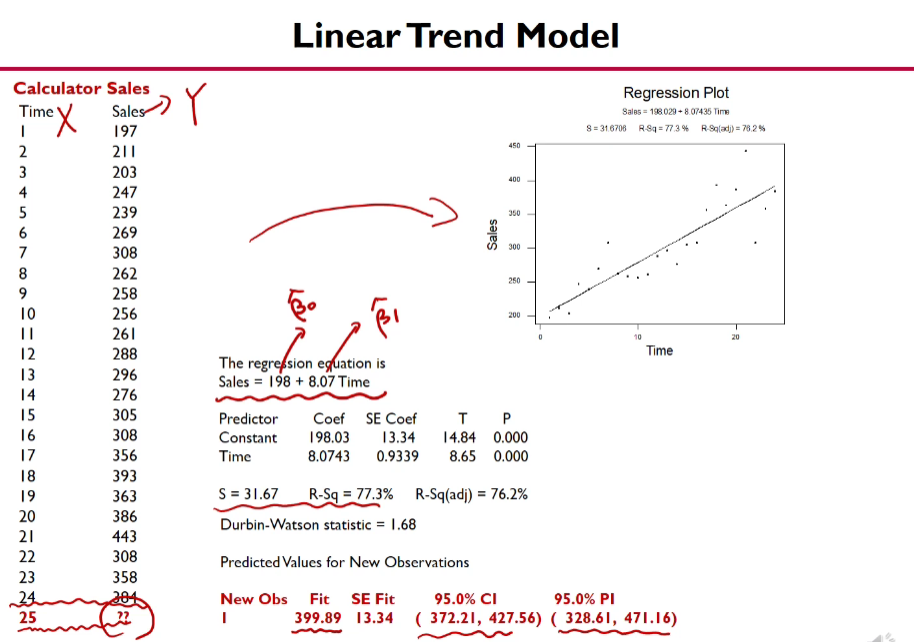
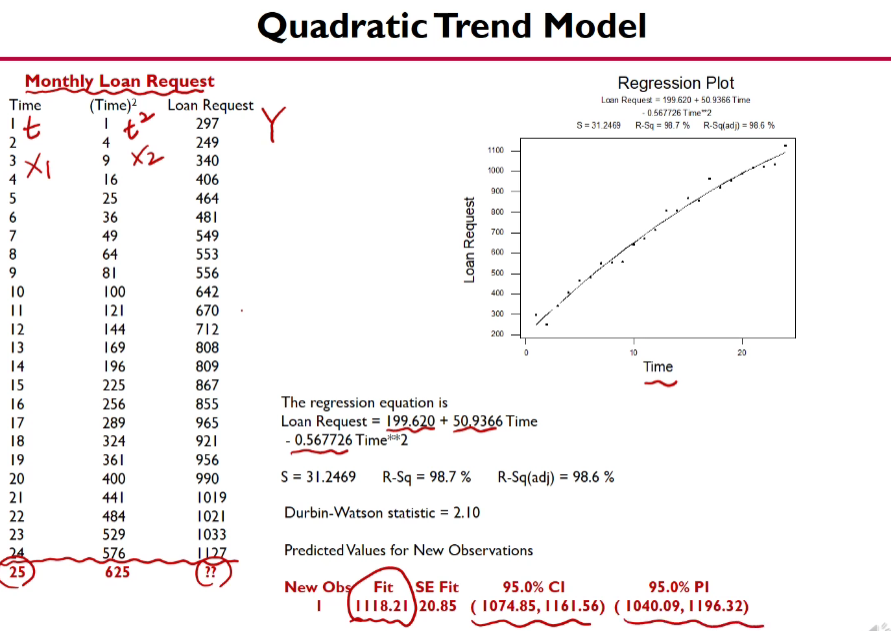
Ordinary Regression Analysis 

 

다음에 해볼 실험 - 선형 모델링 using python
[시계열 분석] 2. 최소 제곱법을 이용한 시계열 분석 with Python (tistory.com)