해당 글은 아래의 위키독스를 기반으로 학습 후, 요약정리한 내용입니다.
딥러닝을 이용한 자연어 처리 입문 - https://wikidocs.net/24949
LSA(잠재 의미 분석)
BoW에 기반한 DTM이나 DTM의 단점을 보완하여 단어의 중요도에 따라 가중치를 부여한 TF-IDF는 기본적으로 단어의 빈도 수를 이용한 수치화 방법이기 때문에 단어의 의미를 고려하지 못한다는 단점이 있습니다. LSA는 BoW에 기반한 알고리즘의 한계점을 보완하는 대안으로 제시되었습니다.
LSA를 이해하기 위해서는 아래의 수학적인 개념을 이해해야 합니다.
- 특이값 분해(SVD, Singular Value Decomposition)
- 절단된 특이값 분해(Truncated SVD)
특이값 분해(SVD, Singular Value Decomposition)
해당 파트는 아래의 블로그를 추가적으로 참고했습니다.
공돌이의 수학정리노트 - https://angeloyeo.github.io/2019/08/01/SVD.html
말 그대로 행렬의 특이값을 추출하기 위한 분해를 수행하는 것을 의미합니다. 특이값 분해를 이해하기 위해서는 특이값 분해에서 사용하는 전제뿐만 아니라, 직교행렬, 대각행렬 등과 같은 개념도 알아야합니다.
- 전제: 실수 벡터 공간(일반적으로는 복소수 공간에 대해 정의함)
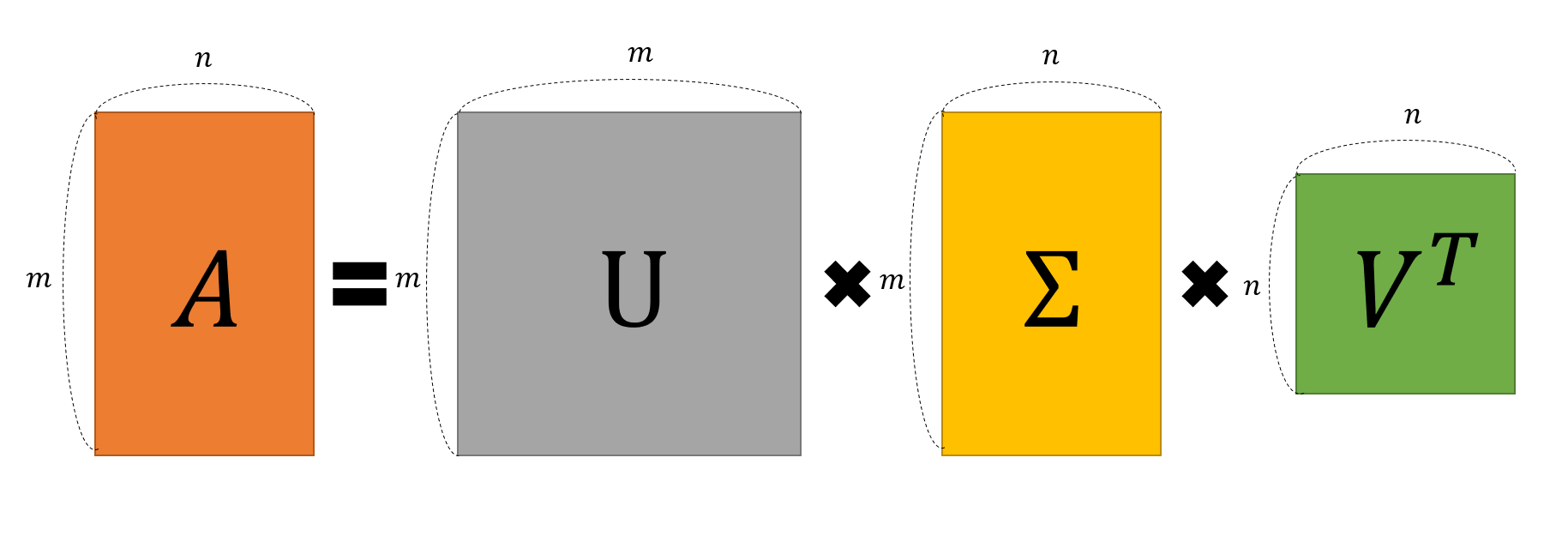
- $A=UΣV^\text{T}$
- $A=m*n\ \text{직사각행렬}$
- $U: m × m\ \text{직교행렬}\ (AA^\text{T}=U(ΣΣ^\text{T})U^\text{T})$
- $V: n × n\ \text{직교행렬}\ (A^\text{T}A=V(Σ^\text{T}Σ)V^\text{T})$
- $Σ: m × n\ \text{직사각 대각행렬}$
- 직교행렬: 자신과 자신의 전치 행렬(대각 성분을 기준으로 행과 열의 성분 바뀐 행렬)의 곱이 단위행렬이 되는 행렬
- $A^{T}\ ×\ A = I$와 $A^{-1}=A^{T}$ 만족하는 행렬
- 대각행렬: 주대각성분 이외에 모든 성분이 0인 행렬
따라서 SVD를 통해 나온 대각행렬의 대각 원소의 값은 행렬 A의 특이값(Singular Value)입니다. 이와 같은 특이값 분해의 기하학적 의미는 직교하는 벡터 공간에 대해 선형 변환 후에 그 크기는 변하지만 여전히 직교할 수 있는 직교 집합을 구하는 것으로 볼 수 있습니다.
- $V$: 선형 변환 전의 임의의 직교하는 벡터들의 열벡터 모음
- $U$: $A$라는 행렬을 통해 선형 변환 후에도, 직교하는 벡터에 대해 각각 크기를 1로 정규화한 벡터들의 열벡터 모음
- $Σ$: 대각 성분이 Singular Value(=Scaling factor)이며, 내림차순으로 정렬된 행렬
- Singular Value를 Scaling Factor라고도 하는 이유는 크기의 변화를 의미하기 때문이다.
위와 같은 기하학적 정의로 생각할 때는 $AV=UΣ$로 볼 수 있습니다. 여기서 V행렬이 직교하는 벡터들의 열벡터 모음이기 때문에 직교행렬이라는 특성을 활용해 전치행렬을 양측에 곱해주면 $A=UΣV^\text{T}$를 도출해낼 수 있습니다.
이러한 특이값 분해는 임의의 행렬에 대해서 해당 행렬과 동일한 크기를 갖는 여러개의 행렬로 분해해서 생각해볼 수 있고, 그 분해된 각 행렬의 원소 값의 크기는 특이값에 의해 결정된다는 것을 알 수 있습니다. 특이값의 개수에 따라 행렬 크기가 결정되기 때문에 임의의 행렬을 부분 복원하는데도 SVD는 사용됩니다. SVD를 이용하면 임의의 행렬을 정보량에 따라 여러 Layer로 쪼개서 생각해줄 수 있게 해준다는 장점이 있습니다.
절단된 특이값 분해(Truncated SVD)
특이값 분해에서 몇개의 Singular Value까지 고려하느냐에 따라 SVD를 활용해 부분 복원을 할 수 있습니다. 절단된 특이값 분해는 대각행렬인 $Σ$의 대각 원소 중에서 상위값을 t개만 남기고 이에 따라 $U$ 행렬과 $V$ 행렬도 t열까지만 남게 합니다. 토픽 모델링에서 사용되는 LSA의 경우 t값을 토픽의 개수를 반영한 하이퍼 파라미터 값으로 둡니다. t값을 크게 하면 다양한 의미를 가져갈 수 있지만 노이즈까지 모두 반영된다는 단점이 있고, t값을 작게 잡으면 노이즈를 제거할 수 있다는 장점이 있습니다. 절단된 특이값 분해는 일부 벡터들을 삭제하는 데이터의 차원을 줄이는 과정을 통해 계산 비용을 줄이는 효과 또한 가져옵니다.
따라서 LSA는 DTM이나 TF-IDF된 행렬에 특이값 분해(SVD)를 적용하여 U, Transposed V, SUM을 각각 얻습니다.
- $U$: 잠재 의미를 표현하기 위해 수치화된 각각의 문서 벡터로 이뤄진 행
- $V^\text{T}$: 토픽 개수($t$) x 단어의 개수 크기, 잠재 의미를 표현하기 위해 수치화 된 각각의 단어 벡터로 이뤄진 열
한계점
LSA는 단순한 구현 수준과 단어의 잠재적인 의미를 이끌어낼 수 있기 때문에 유사도 계산에 유용하다는 장점이 있습니다. 하지만, SVD 특성상 이미 계산된 LSA에 새로운 데이터를 추가하여 계산하려면 처음부터 다시 계산해야하서 새로운 정보에 대해서는 업데이트가 어렵다는 단점이 있습니다. 그래서 LSA의 한계점을 개선한 Word2Vec 등 단어 의미를 벡터화하는 인공신경망 방법론이 등장합니다.
![[Topic Modeling] LSA(잠재 의미 분석)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fc4Gri6%2FbtrfVtzSEDm%2FBuAqyrOavkRNq5PQNDZNw1%2Fimg.png)